Off-Axis Parabolic Mirrors with Through Holes, UV-Enhanced Aluminum Coating

- Centered Hole for Superposition of Two Beams
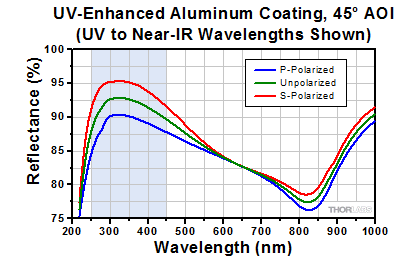
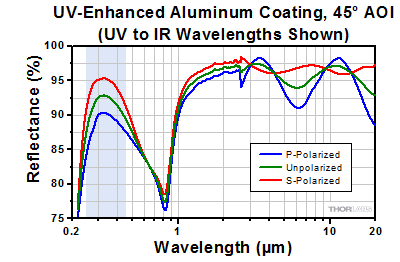
- UV-Enhanced Aluminum Coating for 250 - 450 nm
- Available with Reflected Focal Lengths of 2", 4", or 6"
- SM-Threaded, Unthreaded, and Post-Mountable Adapters
Provide Flexible Mounting Options
MPD229H-F01
Ø2", RFL = 2"
MPD269V-F01
Ø2", RFL = 6"
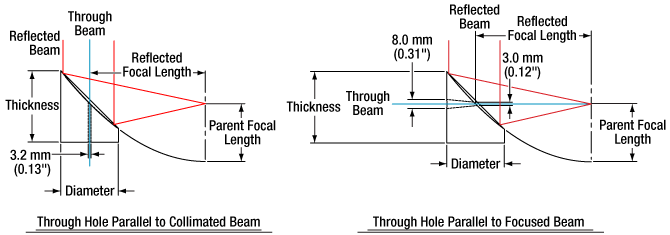
Through Beam is Parallel to Focused Beam
Through Beam is Parallel to Collimated Beam

Please Wait

Click to Enlarge
After initial fabrication, all of our off-axis parabolic mirrors are finished on our single-point diamond turning machine. Visit our Custom Mirrors tab for more information.
Click to Enlarge
Base View of Hole Parallel to Collimated Beam

Click to Enlarge
Back View of Hole Parallel to Focused Beam
Features
- Centered Hole for Through Beam
- Two Hole Orientations Available
- Parallel to Focused Beam: Ø8 mm Entrance Hole in Back Tapers Down to Ø3 mm Hole in Mirror Surface
- Parallel to Collimated Beam: Ø3.2 mm Hole from the Mirror Surface to the Flat Base
- Reflected Beam is Focused without Spherical or Chromatic Aberrations
- UV-Enhanced Aluminum Coating Offers >90% Average Reflectance from 250 - 450 nm
- Reflected Focal Lengths: 2'', 4", or 6"
- Surface Roughness: <100 Å (RMS)
- Three Kinds of Mounting Adapters for Ø2" Mirrors:
- Externally SM-Threaded
- Unthreaded for Use in Mirror Mounts
- With 8-32 (M4) Taps for Post Mounting
- Custom Off-Axis Parabolas with Holes Available (Contact Tech Support)
Thorlabs' Off-Axis Parabolic (OAP) Mirrors with Holes are designed for applications that require two beams to propagate collinearly through space. Each mirror’s reflective surface can achromatically focus a collimated beam or collimate a point source, while the off-axis design separates the focal point from the rest of the beam path. Two hole orientations are available: parallel to the focused beam or parallel to the collimated beam.
Mirrors with holes that allow a through beam to be combined with a focused reflected beam are denoted by item #s that include an “H.” The Ø8 mm hole in the back of the substrate tapers down to a Ø3 mm hole as it approaches the mirror surface, permitting the through beam to be focused by a lens as it propagates. These mirrors are often used in electro-optic sampling measurements and other pump-probe experiments, such as time-resolved terahertz spectroscopy (TRTS). In these experiments, it is necessary to illuminate the electro-optic crystal with a pump beam passing through the parabola so that it overlaps with the focus of the THz probe beam that is reflected off of the surface of the parabola.
Mirrors with holes that allow a through beam to be combined with a collimated reflected beam are denoted by item #s that include a “V.” The Ø3.2 mm bore is large enough to accept a beam from our HeNe lasers. Due to the hole passing through the base of the part, these mirrors cannot be used with any of our OAP mirror mounting adapters. Instead, our smooth bore mounting adapters can be used to mount these parts.
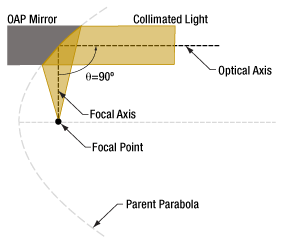
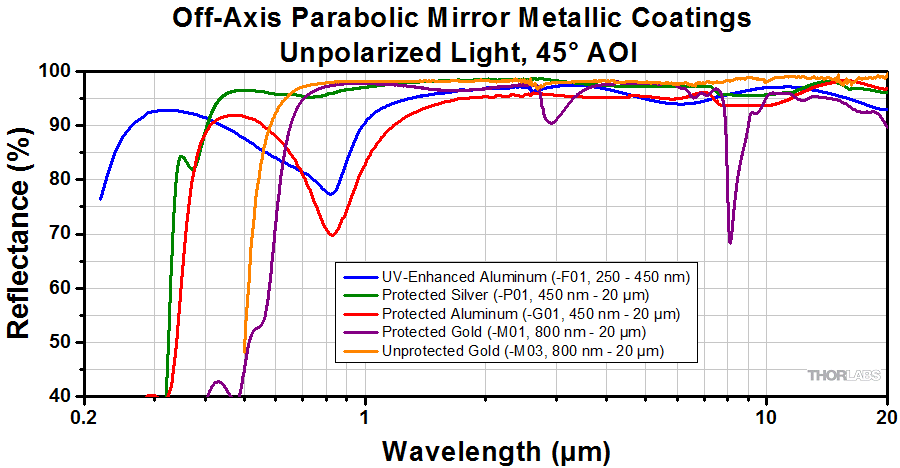
As with the rest of our off-axis parabolas, these mirrors are segments of a parent paraboloid. They achromatically focus a collimated beam, and their reflective design eliminates phase delays and absorption losses introduced by transmissive optics. This makes them well suited for use with femtosecond pulsed lasers. The angle between the focused beam and the collimated beam (off-axis angle) is 90°. As shown in the diagrams above, the collimated beam should be normal to the base of the substrate to achieve a proper focus. The diamond-turned parabolic surface has a UV-enhanced aluminum coating that provides >90% average reflectance from 250 - 450 nm (see the Graphs tab for a plot of the coating performance).
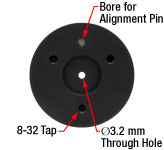
The OAP mirrors are fabricated using aluminum substrates. The base of each mirror has three tapped mounting holes in a triangle pattern and an alignment hole. For OAP mirrors with holes parallel to the focused beam, the holes in the base can be used with a mounting adapter (see the OAP Mounting tab for more details). Holes parallel to the collimated beam pass through the base of the OAP mirror, so mounting adapters cannot be used with these parts. The non-optical surfaces are black-anodized and laser-engraved with the item number for easy identification as shown in the image to the right. The interiors of both types of through holes are not anodized.
| Common Specifications | |
|---|---|
| Metalic Coating | UV-Enhanced Aluminum |
| Reflectance (Average) | >90% Average Reflectance from 250 - 450 nm |
| Off-Axis Angle | 90° |
| Clear Aperture | >90% of Diametera, Not Including Hole |
| Surface Roughness (RMS) | <100 Å |
| Surface Quality | 40-20 Scratch-Dig |
| Parent Focal Length Tolerance | ±1% |
| Reflected Focal Length Tolerance | ±1% |
| Mounting Holesb | 8-32 Taps in Radial Pattern (3 Places) |
| Substrate | Aluminum |
| Manufacturing Process | Diamond Turned |
| Item # | Diametera | Thicknessa | RFLa,b | PFLa,c | Hole Orientationa | Hole Diametera | Reflected Wavefront Error |
|---|---|---|---|---|---|---|---|
| MPD229H-F01 | 2" (50.8 mm) | 2.47" (62.8 mm) | 2" (50.8 mm) | 1" (25.4 mm) | Parallel to Focused Beam |
3 mm on Coated Surface 8 mm on Back of Substrate |
<λ/2 RMS at 633 nm |
| MPD249H-F01 | 2" (50.8 mm) | 2.47" (62.8 mm) | 4" (101.6 mm) | 2" (50.8 mm) | <λ/4 RMS at 633 nm | ||
| MPD269H-F01 | 2" (50.8 mm) | 2.47" (62.8 mm) | 6" (152.4 mm) | 3" (76.2 mm) | |||
| MPD249V-F01 | 2" (50.8 mm) | 2.47" (62.8 mm) | 4" (101.6 mm) | 2" (50.8 mm) | Parallel to Collimated Beam |
3.2 mm (0.13") | |
| MPD269V-F01 | 2" (50.8 mm) | 2.47" (62.8 mm) | 6" (152.4 mm) | 3" (76.2 mm) |
The shaded regions in the graphs denotes the ranges over which we guarantee the specified reflectance. Please note that the reflectance outside of these bands is typical and can vary from lot to lot, especially in out-of-band regions where the reflectance is fluctuating or sloped.
Video Insight: How to Align an Off-Axis Parabolic (OAP) Mirror
Choosing the right mounting adapter is the first step in aligning an OAP mirror. Guidance on how to select the right mounting adapter is located below. For information on how to align an OAP mirror, watch our video to the right.
Mounting Adapters Selection Guide
The bottom of each off-axis parabolic (OAP) mirror contains three tapped mounting holes in a triangle pattern and an alignment hole. These holes are used to attach our Mounting Adapters, which contain three corresponding counterbore holes or captive screws and an alignment pin (see the image to the right). Together, these features allow our OAP mirrors to be securely mounted. The tapped holes are also useful in OEM applications.
We offer three types of mounting plates for Ø1/2", Ø1", and Ø2" OAP mirrors. The first type is designed to be mounted in any Ø1", Ø2", or Ø3" mirror mount, depending upon the diameter of the OAP mirror. The second type, designed for post mounting, contains an 8-32 (M4) tapped hole on all four sides for direct mechanical compatibility with Ø1/2" Posts. The third type is externally SM threaded for direct compatibility with any of our internally SM-threaded components, such as our rotation mounts. For Ø1" 90° OAP mirrors, the KCB1P(/M) right-angle mount allows for cage system integration. The table below shows all of these options.
Our Ø1/2", Ø1", and Ø2" OAP mirrors can also be adapted to our SM threads by placing them into our SM Thread to Double Bore Adapters. This type of adapter allows rotation of the OAP mirror with respect to the adapter prior to securing its position, whereas when using the SM-threaded adapters offered on this page, the final location of the OAP mirror is dictated either by the threads themselves (when fully threaded into a mount) or by using the provided retaining ring to secure it in place.
For Ø3" OAP mirrors, we offer the SM2MP3 mounting adapter, which contains four 8-32 tapped holes for post mounting and has external SM2 threading for mounting in our SM2-threaded components, such as the K6X2 6-axis kinematic mount.
Alternatively, all of our OAP mirrors may be directly mounted in our Precision Kinematic Mirror Mounts using their outer diameter.
| OAP Mirror Mounting Adapters | |||||
|---|---|---|---|---|---|
| Adapter Type | Example Photo (Click to Enlarge) |
OAP Mirror Diameter | |||
| 1/2" | 1" | 2" | 3" | ||
| Smooth Bore |  |
MP127P1 For Ø1" Mounts |
MP254P1 For Ø2" Mounts |
MP508P1a For Ø3" Mounts |
- |
| Post Mounting |  |
MP127P2(/M) 8-32 (M4) Taps |
MP254P2(/M) 8-32 (M4) Taps |
MP508P2(/M)a 8-32 (M4) Taps |
SM2MP3 8-32 Taps |
| SM-Threaded |  |
SM05MP External SM05 (0.535"-40) |
SM1MP External SM1 (1.035"-40) |
SM2MPa External SM2 (2.035"-40) |
SM2MP3 External SM2 (2.035"-40) |
| Right-Angle OAP Mirror Mount |
 |
- | KCB1P(/M) 30 mm Cage Compatible 1/4"-20 (M6) Tap |
- | - |
Selecting a Mirror Based on Desired Output Beam Diameter
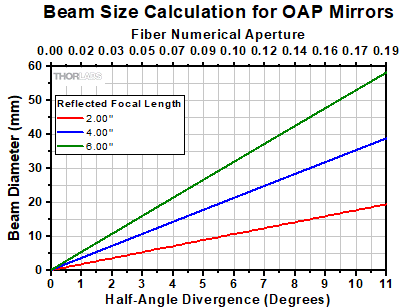
When using an off-axis parabolic mirror to collimate a point source, selection of the appropriate mirror is often done based on the desired output beam diameter. Beam diameter can be calculated using the divergence half-angle of the incident light (Θ) and the reflected focal length of the OAP. To calculate the beam diameter in the small angle approximation, use the following equation:
Beam Diameter = 2 x sin(Θ) x Reflected Focal Length
If you are collimating from a fiber, the equation can be rewritten as:
Beam Diameter = 2 x NA (Fiber) x Reflected Focal Length
The graph to the right visualizes the equations above, showing the relationship between the point source's divergence and collimated beam diameter. Each line represents an OAP with a particular reflected focal length. Not listed here is the diameter of the OAP. The clear aperture of the OAP you select should be larger than the desired beam output diameter.
| Damage Threshold Specifications | |
|---|---|
| Coating Designation (Item # Suffix) | Damage Threshold |
| -F01 (Pulsed) | 0.3 J/cm2 (355 nm, 10 ns, 10 Hz, Ø0.414 mm) 0.2 J/cm2 (1064 nm, 10 ns, 10 Hz, Ø1 mm) |
Damage Threshold Data for Thorlabs' UV-Enhanced Aluminum Coating, Off-Axis Parabolic Mirrors
The specifications to the right are measured data for Thorlabs' UV-enhanced aluminum coating, off-axis parabolic mirrors. Damage threshold specifications are constant for this coating type, regardless of the focal length of the mirror.
Laser Induced Damage Threshold Tutorial
The following is a general overview of how laser induced damage thresholds are measured and how the values may be utilized in determining the appropriateness of an optic for a given application. When choosing optics, it is important to understand the Laser Induced Damage Threshold (LIDT) of the optics being used. The LIDT for an optic greatly depends on the type of laser you are using. Continuous wave (CW) lasers typically cause damage from thermal effects (absorption either in the coating or in the substrate). Pulsed lasers, on the other hand, often strip electrons from the lattice structure of an optic before causing thermal damage. Note that the guideline presented here assumes room temperature operation and optics in new condition (i.e., within scratch-dig spec, surface free of contamination, etc.). Because dust or other particles on the surface of an optic can cause damage at lower thresholds, we recommend keeping surfaces clean and free of debris. For more information on cleaning optics, please see our Optics Cleaning tutorial.
Testing Method
Thorlabs' LIDT testing is done in compliance with ISO/DIS 11254 and ISO 21254 specifications.
First, a low-power/energy beam is directed to the optic under test. The optic is exposed in 10 locations to this laser beam for 30 seconds (CW) or for a number of pulses (pulse repetition frequency specified). After exposure, the optic is examined by a microscope (~100X magnification) for any visible damage. The number of locations that are damaged at a particular power/energy level is recorded. Next, the power/energy is either increased or decreased and the optic is exposed at 10 new locations. This process is repeated until damage is observed. The damage threshold is then assigned to be the highest power/energy that the optic can withstand without causing damage. A histogram such as that below represents the testing of one BB1-E02 mirror.

The photograph above is a protected aluminum-coated mirror after LIDT testing. In this particular test, it handled 0.43 J/cm2 (1064 nm, 10 ns pulse, 10 Hz, Ø1.000 mm) before damage.
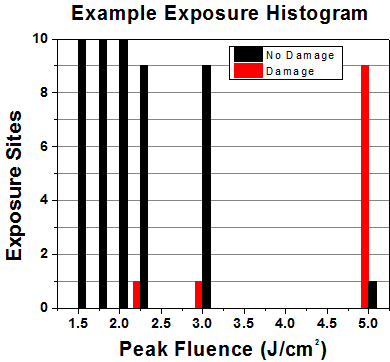
| Example Test Data | |||
|---|---|---|---|
| Fluence | # of Tested Locations | Locations with Damage | Locations Without Damage |
| 1.50 J/cm2 | 10 | 0 | 10 |
| 1.75 J/cm2 | 10 | 0 | 10 |
| 2.00 J/cm2 | 10 | 0 | 10 |
| 2.25 J/cm2 | 10 | 1 | 9 |
| 3.00 J/cm2 | 10 | 1 | 9 |
| 5.00 J/cm2 | 10 | 9 | 1 |
According to the test, the damage threshold of the mirror was 2.00 J/cm2 (532 nm, 10 ns pulse, 10 Hz, Ø0.803 mm). Please keep in mind that these tests are performed on clean optics, as dirt and contamination can significantly lower the damage threshold of a component. While the test results are only representative of one coating run, Thorlabs specifies damage threshold values that account for coating variances.
Continuous Wave and Long-Pulse Lasers
When an optic is damaged by a continuous wave (CW) laser, it is usually due to the melting of the surface as a result of absorbing the laser's energy or damage to the optical coating (antireflection) [1]. Pulsed lasers with pulse lengths longer than 1 µs can be treated as CW lasers for LIDT discussions.
When pulse lengths are between 1 ns and 1 µs, laser-induced damage can occur either because of absorption or a dielectric breakdown (therefore, a user must check both CW and pulsed LIDT). Absorption is either due to an intrinsic property of the optic or due to surface irregularities; thus LIDT values are only valid for optics meeting or exceeding the surface quality specifications given by a manufacturer. While many optics can handle high power CW lasers, cemented (e.g., achromatic doublets) or highly absorptive (e.g., ND filters) optics tend to have lower CW damage thresholds. These lower thresholds are due to absorption or scattering in the cement or metal coating.
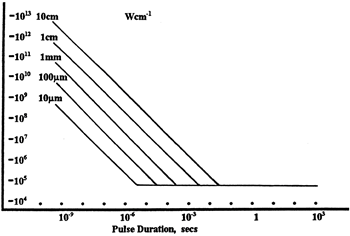
LIDT in linear power density vs. pulse length and spot size. For long pulses to CW, linear power density becomes a constant with spot size. This graph was obtained from [1].
Pulsed lasers with high pulse repetition frequencies (PRF) may behave similarly to CW beams. Unfortunately, this is highly dependent on factors such as absorption and thermal diffusivity, so there is no reliable method for determining when a high PRF laser will damage an optic due to thermal effects. For beams with a high PRF both the average and peak powers must be compared to the equivalent CW power. Additionally, for highly transparent materials, there is little to no drop in the LIDT with increasing PRF.
In order to use the specified CW damage threshold of an optic, it is necessary to know the following:
- Wavelength of your laser
- Beam diameter of your beam (1/e2)
- Approximate intensity profile of your beam (e.g., Gaussian)
- Linear power density of your beam (total power divided by 1/e2 beam diameter)
Thorlabs expresses LIDT for CW lasers as a linear power density measured in W/cm. In this regime, the LIDT given as a linear power density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size, as demonstrated by the graph to the right. Average linear power density can be calculated using the equation below.

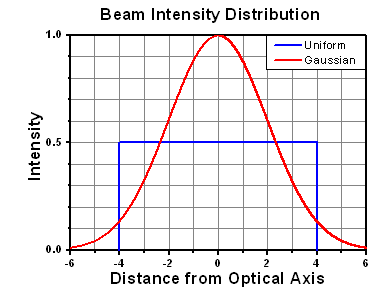
The calculation above assumes a uniform beam intensity profile. You must now consider hotspots in the beam or other non-uniform intensity profiles and roughly calculate a maximum power density. For reference, a Gaussian beam typically has a maximum power density that is twice that of the uniform beam (see lower right).
Now compare the maximum power density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately. A good rule of thumb is that the damage threshold has a linear relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 10 W/cm at 1310 nm scales to 5 W/cm at 655 nm):

While this rule of thumb provides a general trend, it is not a quantitative analysis of LIDT vs wavelength. In CW applications, for instance, damage scales more strongly with absorption in the coating and substrate, which does not necessarily scale well with wavelength. While the above procedure provides a good rule of thumb for LIDT values, please contact Tech Support if your wavelength is different from the specified LIDT wavelength. If your power density is less than the adjusted LIDT of the optic, then the optic should work for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. The damage analysis will be carried out on a similar optic (customer's optic will not be damaged). Testing may result in additional costs or lead times. Contact Tech Support for more information.
Pulsed Lasers
As previously stated, pulsed lasers typically induce a different type of damage to the optic than CW lasers. Pulsed lasers often do not heat the optic enough to damage it; instead, pulsed lasers produce strong electric fields capable of inducing dielectric breakdown in the material. Unfortunately, it can be very difficult to compare the LIDT specification of an optic to your laser. There are multiple regimes in which a pulsed laser can damage an optic and this is based on the laser's pulse length. The highlighted columns in the table below outline the relevant pulse lengths for our specified LIDT values.
Pulses shorter than 10-9 s cannot be compared to our specified LIDT values with much reliability. In this ultra-short-pulse regime various mechanics, such as multiphoton-avalanche ionization, take over as the predominate damage mechanism [2]. In contrast, pulses between 10-7 s and 10-4 s may cause damage to an optic either because of dielectric breakdown or thermal effects. This means that both CW and pulsed damage thresholds must be compared to the laser beam to determine whether the optic is suitable for your application.
| Pulse Duration | t < 10-9 s | 10-9 < t < 10-7 s | 10-7 < t < 10-4 s | t > 10-4 s |
|---|---|---|---|---|
| Damage Mechanism | Avalanche Ionization | Dielectric Breakdown | Dielectric Breakdown or Thermal | Thermal |
| Relevant Damage Specification | No Comparison (See Above) | Pulsed | Pulsed and CW | CW |
When comparing an LIDT specified for a pulsed laser to your laser, it is essential to know the following:
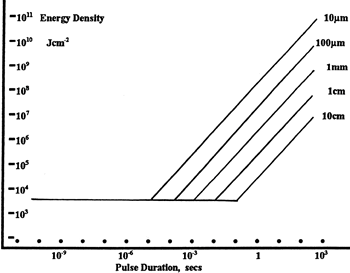
LIDT in energy density vs. pulse length and spot size. For short pulses, energy density becomes a constant with spot size. This graph was obtained from [1].
- Wavelength of your laser
- Energy density of your beam (total energy divided by 1/e2 area)
- Pulse length of your laser
- Pulse repetition frequency (prf) of your laser
- Beam diameter of your laser (1/e2 )
- Approximate intensity profile of your beam (e.g., Gaussian)
The energy density of your beam should be calculated in terms of J/cm2. The graph to the right shows why expressing the LIDT as an energy density provides the best metric for short pulse sources. In this regime, the LIDT given as an energy density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size. This calculation assumes a uniform beam intensity profile. You must now adjust this energy density to account for hotspots or other nonuniform intensity profiles and roughly calculate a maximum energy density. For reference a Gaussian beam typically has a maximum energy density that is twice that of the 1/e2 beam.
Now compare the maximum energy density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately [3]. A good rule of thumb is that the damage threshold has an inverse square root relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 1 J/cm2 at 1064 nm scales to 0.7 J/cm2 at 532 nm):
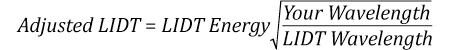
You now have a wavelength-adjusted energy density, which you will use in the following step.
Beam diameter is also important to know when comparing damage thresholds. While the LIDT, when expressed in units of J/cm², scales independently of spot size; large beam sizes are more likely to illuminate a larger number of defects which can lead to greater variances in the LIDT [4]. For data presented here, a <1 mm beam size was used to measure the LIDT. For beams sizes greater than 5 mm, the LIDT (J/cm2) will not scale independently of beam diameter due to the larger size beam exposing more defects.
The pulse length must now be compensated for. The longer the pulse duration, the more energy the optic can handle. For pulse widths between 1 - 100 ns, an approximation is as follows:
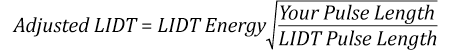
Use this formula to calculate the Adjusted LIDT for an optic based on your pulse length. If your maximum energy density is less than this adjusted LIDT maximum energy density, then the optic should be suitable for your application. Keep in mind that this calculation is only used for pulses between 10-9 s and 10-7 s. For pulses between 10-7 s and 10-4 s, the CW LIDT must also be checked before deeming the optic appropriate for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. Contact Tech Support for more information.
[1] R. M. Wood, Optics and Laser Tech. 29, 517 (1998).
[2] Roger M. Wood, Laser-Induced Damage of Optical Materials (Institute of Physics Publishing, Philadelphia, PA, 2003).
[3] C. W. Carr et al., Phys. Rev. Lett. 91, 127402 (2003).
[4] N. Bloembergen, Appl. Opt. 12, 661 (1973).
In order to illustrate the process of determining whether a given laser system will damage an optic, a number of example calculations of laser induced damage threshold are given below. For assistance with performing similar calculations, we provide a spreadsheet calculator that can be downloaded by clicking the button to the right. To use the calculator, enter the specified LIDT value of the optic under consideration and the relevant parameters of your laser system in the green boxes. The spreadsheet will then calculate a linear power density for CW and pulsed systems, as well as an energy density value for pulsed systems. These values are used to calculate adjusted, scaled LIDT values for the optics based on accepted scaling laws. This calculator assumes a Gaussian beam profile, so a correction factor must be introduced for other beam shapes (uniform, etc.). The LIDT scaling laws are determined from empirical relationships; their accuracy is not guaranteed. Remember that absorption by optics or coatings can significantly reduce LIDT in some spectral regions. These LIDT values are not valid for ultrashort pulses less than one nanosecond in duration.

A Gaussian beam profile has about twice the maximum intensity of a uniform beam profile.
CW Laser Example
Suppose that a CW laser system at 1319 nm produces a 0.5 W Gaussian beam that has a 1/e2 diameter of 10 mm. A naive calculation of the average linear power density of this beam would yield a value of 0.5 W/cm, given by the total power divided by the beam diameter:

However, the maximum power density of a Gaussian beam is about twice the maximum power density of a uniform beam, as shown in the graph to the right. Therefore, a more accurate determination of the maximum linear power density of the system is 1 W/cm.
An AC127-030-C achromatic doublet lens has a specified CW LIDT of 350 W/cm, as tested at 1550 nm. CW damage threshold values typically scale directly with the wavelength of the laser source, so this yields an adjusted LIDT value:

The adjusted LIDT value of 350 W/cm x (1319 nm / 1550 nm) = 298 W/cm is significantly higher than the calculated maximum linear power density of the laser system, so it would be safe to use this doublet lens for this application.
Pulsed Nanosecond Laser Example: Scaling for Different Pulse Durations
Suppose that a pulsed Nd:YAG laser system is frequency tripled to produce a 10 Hz output, consisting of 2 ns output pulses at 355 nm, each with 1 J of energy, in a Gaussian beam with a 1.9 cm beam diameter (1/e2). The average energy density of each pulse is found by dividing the pulse energy by the beam area:
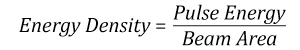
As described above, the maximum energy density of a Gaussian beam is about twice the average energy density. So, the maximum energy density of this beam is ~0.7 J/cm2.
The energy density of the beam can be compared to the LIDT values of 1 J/cm2 and 3.5 J/cm2 for a BB1-E01 broadband dielectric mirror and an NB1-K08 Nd:YAG laser line mirror, respectively. Both of these LIDT values, while measured at 355 nm, were determined with a 10 ns pulsed laser at 10 Hz. Therefore, an adjustment must be applied for the shorter pulse duration of the system under consideration. As described on the previous tab, LIDT values in the nanosecond pulse regime scale with the square root of the laser pulse duration:
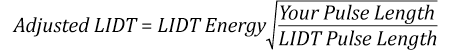
This adjustment factor results in LIDT values of 0.45 J/cm2 for the BB1-E01 broadband mirror and 1.6 J/cm2 for the Nd:YAG laser line mirror, which are to be compared with the 0.7 J/cm2 maximum energy density of the beam. While the broadband mirror would likely be damaged by the laser, the more specialized laser line mirror is appropriate for use with this system.
Pulsed Nanosecond Laser Example: Scaling for Different Wavelengths
Suppose that a pulsed laser system emits 10 ns pulses at 2.5 Hz, each with 100 mJ of energy at 1064 nm in a 16 mm diameter beam (1/e2) that must be attenuated with a neutral density filter. For a Gaussian output, these specifications result in a maximum energy density of 0.1 J/cm2. The damage threshold of an NDUV10A Ø25 mm, OD 1.0, reflective neutral density filter is 0.05 J/cm2 for 10 ns pulses at 355 nm, while the damage threshold of the similar NE10A absorptive filter is 10 J/cm2 for 10 ns pulses at 532 nm. As described on the previous tab, the LIDT value of an optic scales with the square root of the wavelength in the nanosecond pulse regime:
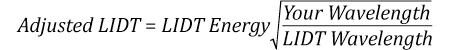
This scaling gives adjusted LIDT values of 0.08 J/cm2 for the reflective filter and 14 J/cm2 for the absorptive filter. In this case, the absorptive filter is the best choice in order to avoid optical damage.
Pulsed Microsecond Laser Example
Consider a laser system that produces 1 µs pulses, each containing 150 µJ of energy at a repetition rate of 50 kHz, resulting in a relatively high duty cycle of 5%. This system falls somewhere between the regimes of CW and pulsed laser induced damage, and could potentially damage an optic by mechanisms associated with either regime. As a result, both CW and pulsed LIDT values must be compared to the properties of the laser system to ensure safe operation.
If this relatively long-pulse laser emits a Gaussian 12.7 mm diameter beam (1/e2) at 980 nm, then the resulting output has a linear power density of 5.9 W/cm and an energy density of 1.2 x 10-4 J/cm2 per pulse. This can be compared to the LIDT values for a WPQ10E-980 polymer zero-order quarter-wave plate, which are 5 W/cm for CW radiation at 810 nm and 5 J/cm2 for a 10 ns pulse at 810 nm. As before, the CW LIDT of the optic scales linearly with the laser wavelength, resulting in an adjusted CW value of 6 W/cm at 980 nm. On the other hand, the pulsed LIDT scales with the square root of the laser wavelength and the square root of the pulse duration, resulting in an adjusted value of 55 J/cm2 for a 1 µs pulse at 980 nm. The pulsed LIDT of the optic is significantly greater than the energy density of the laser pulse, so individual pulses will not damage the wave plate. However, the large average linear power density of the laser system may cause thermal damage to the optic, much like a high-power CW beam.
Custom Off-Axis Parabolic (OAP) and Aspheric Mirrors
Key Capabilities
- Nanotech® 450UPL Ultra Precision 3-Axis CNC Diamond Turning Lathe for Individual Custom Mirrors
- Custom Sizes, Focal Lengths, Substrates, Coatings, and Clearance Holes
- Off- and On-Axis Parabolic, Conical, and Toroidal Mirrors
- Biconic Surfaces and Irregular Aspheric Optics
Thorlabs' advanced single-point diamond turning capabilities allow us to produce custom OAP and aspheric mirrors in small quantities. We can produce long focal length and large diameter optics, as well as optics with custom shapes.

Click to Enlarge
We offer OAP mirrors with custom sizes, focal lengths, substrates, coatings, and clearance holes.
In addition to our stock off-axis parabolic (OAP) mirrors, Thorlabs is also capable of manufacturing a variety of custom aspheric mirrors. Our unique single-point diamond turning (SPDT) capabilities allow us to produce these customs in low quantities at prices that are comparable with our stock offerings. As shown in the video to the right, we engage the slow-slide-servo process of our SPDT machine to polish individual off-axis mirrors by synchronizing the rotational position of the spindle with the linear position of the translation axes.
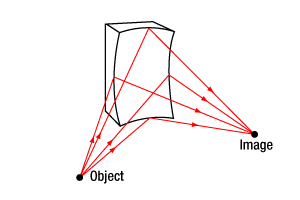
Click to Enlarge
Toroidal mirrors have two different radii of curvature and are used to image off-axis points without introducing astigmatism.
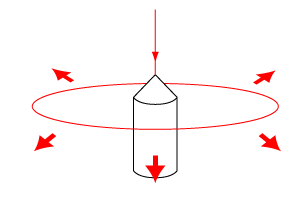
Click to Enlarge
Conical mirrors provide 360° of illumination.
This unique manufacturing capability allows us to provide OAP mirrors with custom reflected focal lengths and diameters, including long-focal-length and large-diameter optics that cannot be produced by conventional two-axis machining. In addition, we can produce OAP mirrors with a variety of custom substrates (including copper), custom coatings, and custom hole sizes and shapes. The use of copper substrates and other advanced techniques also allow us to offer OAP mirrors with enhanced finishes that exhibit less surface roughness than our our stock products, resulting in improved wavefront quality.
Our SPDT competency also enables us to produce mirrors with other custom biconic surfaces and aspheric shapes, including on-axis parabolic, conical, and toroidal mirrors. These custom mirror shapes can be used in a wide variety of optical instruments and specialized imaging systems. For example, toroidal mirrors, which are used to image off-axis points without introducing astigmatism, are commonly used in compact Czerny-Turner monochromators. Conical mirrors, on the other hand, are ideal for non-imaging applications that require 360° of uniform illumination.
We are generally able to produce custom OAP mirrors and aspheric mirrors with short lead times. For modifications to an existing part, delivery in 4-6 weeks is standard. For custom shapes and long focal length optics, a 6-8 week lead time is typical. To receive more information or a quote for a custom optic, please contact Tech Support.
Our engineers are available to help manufacture optics for your application.
Customs are available in low quantities at prices that are comparable with our stock catalog products.
Please contact techsupport@thorlabs.com with your custom optic requests.
Insights into Off-Axis Parabolic Mirrors
Scroll down to read about the unique properties of off-axis parabolic (OAP) mirrors and how to take advantage of them:
- The Off-Axis Angle
- Locating the Optical and Focal Axes of an OAP
Click here for more insights into lab practices and equipment.
The Off-Axis Angle
Click to Enlarge
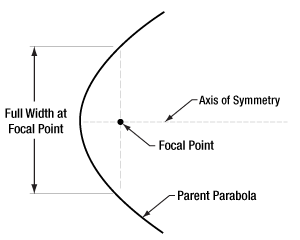
Figure 2: It is common to measure the width of the parabola with respect to a line that passes through the focus and is perpendicular to the axis.
Click to Enlarge
Figure 1: One section of the parent parabola provides a 90° off-axis angle.
Click to Enlarge
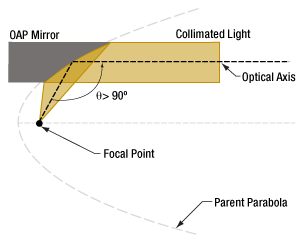
Figure 4: Decreasing the width of the parabola increases the off-axis angle. For example, compare this illustration with Figure 2.
Click to Enlarge
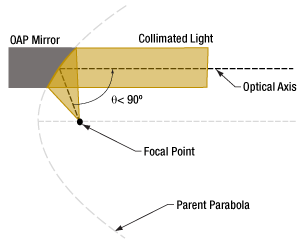
Figure 3: Choosing a section closer to the axis of the parabola results in a smaller off-axis angle.
The off-axis angle ( θ ) of an OAP mirror is measured between the mirror's optical and focal axes. The OAP mirror in Figure 1 has a 90° angle.
The angle depends on the segment of the parent parabola used for the OAP mirror, as well as the width (Figure 2) of the parent parabola.
Proximity of Parabolic Segment and Focal Point
Choosing a segment of the parent parabola closer to the focal point reduces the off-axis angle. The mirror in Figure 3 has a smaller angle than the one in Figure 2, but the only difference between them is that the section of the parabola selected for the OAP mirror in Figure 3 is closer to the focal point.
The location of the parabolic segment also controls the focal length. Choosing a parabolic segment closer to the focal point results in a shorter distance between the center of the mirror and the focal point.
Width of the Parent Parabola
Increasing the width of the parent parabola decreases the off-axis angle. This inverse relationship is illustrated by Figures 3 and 4. The width of the parabola is larger in Figure 3, and this is also the mirror with a smaller angle.
The width of the parent parabola also affects the focal length. The wider the parabola, the longer the focal length.
Available Off-Axis Angles
OAP mirrors are often designed to have a 90° off-axis angle, but OAP mirrors with angles less than 90° are also common.
Date of Last Edit: Dec. 4, 2019
Locating the Optical and Focal Axes of an OAP
Click to Enlarge
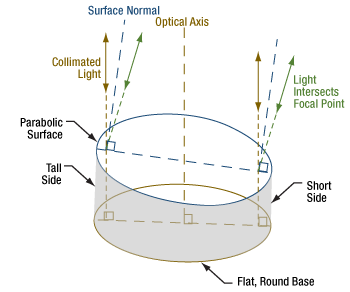
Figure 6: The orientation of the optical axis can be found by noting it is perpendicular to the base of the mirror's substrate. The location of the focal point can be estimated by considering collimated light rays that are directed parallel to the optical axis. These rays reflect symmetrically around the local surface normals and pass through the mirror's focal point.

Click to Enlarge
Figure 5: OAP mirrors have a flat, round base and a side that varies in height around the circumference. The planar base is normal to the mirror's optical axis. Shown above is the MPD2151-P01.
When working with off-axis parabolic (OAP) mirrors, it can be challenging to identify the optical and focal axes. This is particularly true when the parabolic curvature of the surface is hard to see (Figure 5).
The physical characteristics and dimensions of the mirror's substrate can provide a useful guide when positioning and aligning the mirror.
The mirror's substrate has a flat, round base. The optical axis is oriented normal to this planar base. Therefore, collimated light should be directed normal to the surface of the base.
The substrate has a tall side and a short side, and the reflective surface is sloped between them. The surface normal at different points across the reflector can be roughly estimated by visually examining the surface (Figure 6).
The location of the focal point can be estimated by considering a ray of collimated light, parallel to the optical axis, that reflects from the surface of the mirror. The incident ray reflects symmetrically about the surface normal. The reflected ray will pass through the focal point. By mentally tracing two rays from positions close to the tall and short sides of the mirror, respectively, it should be possible to estimate the location of the focal point.
Mounting and Alignment Features on Thorlabs' OAP Mirrors
Thorlabs' OAP mirrors have an alignment hole and three tapped mounting holes machined into the bottom surface of their bases. The pattern of tapped holes matches the vertices of an equilateral triangle, and the position of the smooth-bore alignment hole indicates the short side of the OAP mirror. The tapped holes are designed to secure the mirror to mounting adapters or mounting platforms.
Date of Last Edit: Dec. 4, 2019
| Posted Comments: | |
| No Comments Posted |

| Item # | MPD229H-F01 | MPD249H-F01 | MPD269H-F01 | MPD249V-F01 | MPD269V-F01 |
|---|---|---|---|---|---|
| Diametera | 2" (50.8 mm) | 2" (50.8 mm) | 2" (50.8 mm) | 2" (50.8 mm) | 2" (50.8 mm) |
| Reflected Focal Length (RFL)a | 2" (50.8 mm) | 4" (101.6 mm) | 6" (152.4 mm) | 4" (101.6 mm) | 6" (152.4 mm) |
| Parent Focal Lengtha | 1" (25.4 mm) | 2" (50.8 mm) | 3" (76.2 mm) | 2" (50.8 mm) | 3" (76.2 mm) |
| Hole Orientation | Parallel to Focused Beam | Parallel to Collimated Beamb | |||
| Hole Diameter | 3 mm on Coated Surface 8 mm on Back of Substrate |
3.2 mm (0.13") | |||
| Thicknessa | 2.47" (62.8 mm) | 2.47" (62.8 mm) | 2.47" (62.8 mm) | ||
| Off-Axis Angle | 90° | 90° | |||
| Reflected Wavefront Error | <λ/2 RMS at 633 nm |
<λ/4 RMS at 633 nm | <λ/4 RMS at 633 nm | ||
| Bottom Mounting Holes | Three 8-32 Tapsc | Three 8-32 Tapsb | |||


Click to Enlarge
Ø2" OAP Mirror with Hole Parallel to Focused Beam Mounted on a Ø1/2" Post
Using an MP508P2 Adapter
- Contain Three #8 Counterbores and an Alignment Pin for Mounting to Ø2" OAP Mirrors
- SM2MP: Diameter is Externally SM2 Threaded
- MP508P1: Designed to Fit into Ø3" Mirror Mounts
- MP508P2(/M): Post Mountable in Four Orientations
Our Mounting Adapters for Ø2" Off-Axis Parabolic Mirrors provide mounting alternatives to our smooth bore kinematic mirror mounts. Each contains three #8 counterbores that are positioned to align with the 8-32 tapped holes on our Ø2" OAP Mirrors. Please note that these adapters will block the through holes on OAP Mirrors with holes parallel to the collimated beam. Our smooth bore mounting adapters can be used to mount these parts.
SM2MP
The SM2MP OAP Mirror Adapter is externally SM2 threaded (2.035"-40), which allows a Ø2" OAP mirror to be directly mounted to an internally SM2-threaded component. The adapter is designed to allow easy adaptability to a 60 mm cage system as well as SM2-threaded mirror, translation, and rotation mounts. The included SM2RR retaining ring secures the adapter in place when it is threaded into a mount. An SPW604 and SPW801 Spanner Wrench can be used to thread the retaining ring and adapter, respectively. Three low profile 8-32 cap screws and the required 5/64" hex key are provided with each adapter.
MP508P1
The unthreaded MP508P1 OAP Mirror Adapter is sized to fit inside a Ø3" mirror mount, such as the KS3 Mirror Mount shown above. Three standard 8-32 cap screws and the required 9/64" hex key are provided with each adapter.
MP508P2(/M)
The MP508P2(/M) OAP Mirror Adapter contains four 8-32 (M4) taps, for post mounting, that orient the OAP mirror at right angles. The distance from the center of the optic to the edge of the mount in the MP508P2 is 1.5" (38.1 mm), allowing for standardized optical axis heights when used with a fixed height post, such as our Ø1" Posts. Please note that the MP508P2(/M) is not compatible with Ø3" mirror mounts, and is instead designed for post mounting. Three standard 8-32 cap screws and the required 9/64" hex key are provided with each adapter.
 Products Home
Products Home











 Click to Enlarge
Click to Enlarge


 Zoom
Zoom



 90° UV-Enhanced Aluminum OAPs with Through Holes
90° UV-Enhanced Aluminum OAPs with Through Holes