Extinction Ratio of Light Output by Polarization Maintaining Fiber

What limits the extinction ratio (ER) of light output from PANDA and bow-tie PM fibers?

Click to Enlarge

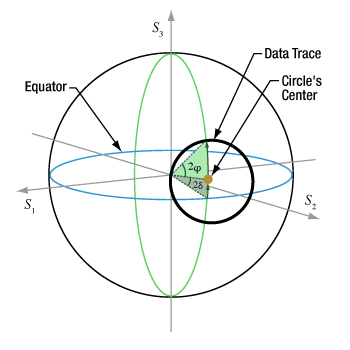
Figure 1: Due to the effects of cross talk, PM fibers typically output light that is slightly elliptically polarized. Varying the temperature applied to a PM fiber will change the output elliptical polarization state in a controlled manner. The polarization measurement values will trace a circle on the Poincaré sphere and can be used to characterize the output light.

Click to Enlarge

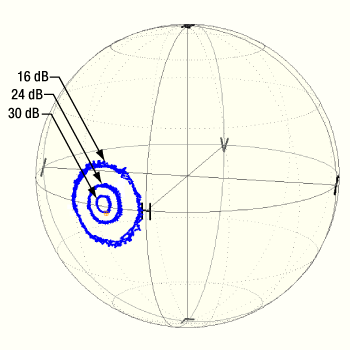
Figure 2: Three different data traces, each corresponding to a different angular mismatch between input linear polarization state and PM fiber axis, are plotted on a Poincaré sphere. Each trace was acquired while using a heat gun to vary the fiber's temperature, which cycled the output polarization state. As the angular mismatch decreased, the range of temperature-dependent polarization states decreased, and the extinction ratio increased. Extinction ratios are given for each trace in decibels (dB)

The extinction ratio (ER) of the light output from a PANDA and bow-tie polarization-maintaining (PM) fiber will be reduced, relative to the ER of input light, due to a combination of non-ideal coupling conditions, the effects of external stress applied to the fiber, and interactions between the light and fiber imperfections. All can worsen (decrease) the ER by transferring some light to the orthogonal polarization state.

Approximate Cross Talk Due to Misalignment
Cross talk (cross coupling) occurs when some fraction of light becomes polarized parallel to the orthogonal direction. Coupling light into a PM fiber can cause cross talk if there is misalignment (rotation) between the polarization axes of the source and the fiber. In this case, the linearly polarized light from the source would be split between two orthogonally polarized components, which are guided separately by the slow and fast axes of the fiber.

Cross talk due to misalignment can be significant, and it can be estimated by varying the fiber's temperature while measuring the output polarization state. If the output light includes both orthogonally polarized components, the delay between them will vary with temperature. This will cause the output light's elliptical polarization to vary with temperature. 

When the temperature-dependent polarization measurements are plotted on a Poincaré sphere, they will trace out a circle (Figures 1 and 2). The approximate value of cross talk due to misalignment can be found from the angle (2φ) of the arc from the point at the circle's center to a point on its circumference.

If the point in the center of the circle is used as a reference, the angle 2φ is the incremental ellipticity needed to reach the circle's circumference. When the half-angle (φ ) is expressed in radians, the approximate amount of cross talk in decibels is,

Cross Talk (dB) ≈ -20 log (tan(φ )).

One way to improve the alignment between the source and fiber is to rotate the polarization angle of the source around the optical axis until the temperature-dependent fluctuations in the fiber's output polarization state are minimized.

Approximating ER of the Output Light
A minimal amount of cross talk will occur as the light propagates down the fiber and interacts with fiber imperfections, but externally applied stress can significantly reduce the ER. Small diameter coils, tightly winding the fiber over bumpy or sharp features, and fixing the bare fiber against hard surfaces can also lower the ER. Fiber connectors can also be a significant source of cross talk, due to the stresses arising from interactions among the bare fiber, connector ferrule, and potting compound.

The extinction ratio (ER) can be calculated using different approximations. One, 

ER_δ (dB) ≈ -20 log (tan(φ + |δ |)).

is similar to the equation used to calculate cross talk due to misalignment but includes cross talk arising from fiber imperfections, microbends, and other perturbations distributed along the length of the fiber. These effects displace the center of the circular trace from the equator of the Poincaré sphere by an angle 2δ. A more exact approximation,

takes into account the degree of polarization (DOP), which is the intensity of polarized light divided by the total light intensity.

References
[1] Chris Emslie, in Specialty Optical Fibers Handbook, edited by Alexis Mendez and T. F. Morse (Elsevier, Inc., New York, 2007) pp. 243-277.
[2] Edward Collett, Polarized Light in Fiber Optics (Elsevier, Inc., New York, 2007) pp. 45-53.