Faraday Rotators

- Rotates Linearly Polarized Light Non-Reciprocally by 45°
- Operating Ranges for Visible or IR Beams
- Mounted in Lens Tubes with SM1 Threading
I405R5
405 nm CWL
I980R5
980 nm CWL
I1064R3
1064 nm CWL
Application Idea
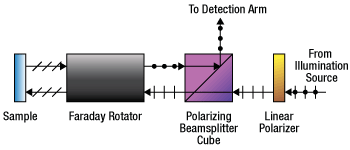
Use a Faraday Rotator with a polarizing beamsplitter to split the illumination and detection arms of a reflectance imaging system.
See Application tab for details.
I2050R5
2050 nm CWL
I780R5
780 nm CWL

Please Wait
 Click to Enlarge
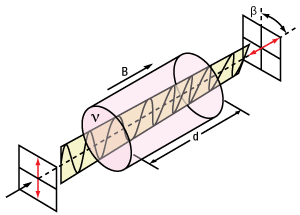
Click to EnlargeLinearly polarized light will rotate β radians after traveling through a faraday rotator with Verdet constant V over d meters when in a magnetic field with flux density B.
Features
- Non-Reciprocal, 45° Rotation of Linearly Polarized Light
- 21 Center Wavelengths from 405 nm to 2050 nm
- Direction of Polarization Rotation Engraved on Housing
- SM1 (1.035"-40) Threading for Integration with Optomechanical Components
- Contact Tech Sales for Custom Faraday Rotators
Faraday Rotators are ferromagnetic crystals surrounded by strong permanent magnets, which form a magneto-optic device. Linearly polarized light sent through a faraday rotator will be rotated by 45° independently of the input angle. Polarization is rotated non-reciprocally, meaning that light entering from the opposite side of the crystal will continue rotating in the same direction relative to the crystal. The rotation direction is indicated by an arrow engraved on the aluminum housing. The entrance and exit faces of our crystals are wedged approximately 1° to 2° and coated with an antireflection coating to reduce back reflections. Each Faraday rotator is designed to operate at a specific center wavelength and at ambient room temperature (approx. 22 °C); operation outside of this range will cause the output rotation angle and/or transmission to fluctuate outside of their specifications.
These devices operate on the Faraday Effect, which can be quantified with the equation β = VBd. The rotation angle, β, is measured in radians and is defined as the product of the crystal's Verdet Constant, V; the magnetic flux density in teslas, B, along the direction of propagation; and the length of the crystal in meters, d. These variables can be seen in the diagram to the right. This effect is taken advantage of in optical isolators (see the Isolator Tutorial tab) and reflectance imaging (see the Application tab). Thorlabs offers a large selection of stocked and custom isolators for free-space and fiber-coupled applications. Please contact Tech Sales if you require a Faraday rotator with a different rotation angle or center wavelength.
Each rotator comes with an SM1CP1 and SM1CP2 end cap; both should be removed before use. Due to the powerful magnets contained in each rotator, these should be kept at least 2" (50.8 mm) away from materials or devices which can be affected or damaged by magnets.
 Click to Enlarge
Click to EnlargeThis section can be used in a reflectance imaging system to split illumination and detection arms via non-reciprocal polarization rotation.
Faraday Rotators for Reflectance Imaging
There are a number of ways to separate the illumination and detection arms of an imaging system. Dichroic mirrors are commonly used to split excitation and emission spectra in fluorescence microscopy. However, some applications, such as reflectance imaging techniques, require on-axis illumination and imaging with a single wavelength of light. One way to accomplish this is by taking advantage of the non-reciprocal nature of Faraday Rotators.
The application photo to the right shows a section that could be used in a reflectance imaging setup. First, a beam of unpolarized 532 nm light can enter the system at the right, incident to a LPVISC100-MP2 linear polarizer. The linearly polarized light can be aligned using the CRM1PT(/M) rotation mount to transmit through the CCM1-PBS25-532-HP(/M) polarizing beamsplitter cube at the center. The light's polarization state is then immediately rotated 45° by the I532R5 Faraday Rotator; the rotational alignment of the Faraday rotator is irrelevant. The light can then be sent to a scanning module or straight to an objective to the sample. The reflected light that retains the incident polarization state will continue to rotate upon reentering the Faraday rotator, making it perpendicular to its original polarization state. This light will be deflected by the polarizing beam splitter into the detection arm of your imaging system for analysis. A setup like this can be mounted directly to an optical table or incorporated into a larger DIY system with our Cerna® microscope components.
 Click to Enlarge
Click to EnlargeA Simplified Diagram of the Setup. Reflected Beam is Offset for Illustrative Purposes Only.
Optical Isolator Tutorial
Function
An optical isolator is a passive magneto-optic device that only allows light to travel in one direction. Isolators are used to protect a source from back reflections or signals that may occur after the isolator. Back reflections can damage a laser source or cause it to mode hop, amplitude modulate, or frequency shift. In high-power applications, back reflections can cause instabilities and power spikes.
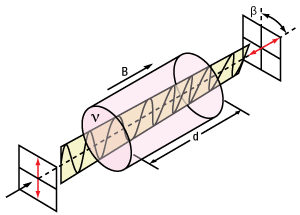
An isolator's function is based on the Faraday Effect. In 1842, Michael Faraday discovered that the plane of polarized light rotates while transmitting through glass (or other materials) that is exposed to a magnetic field. The direction of rotation is dependent on the direction of the magnetic field and not on the direction of light propagation; thus, the rotation is non-reciprocal. The amount of rotation β equals V x B x d, where V, B, and d are as defined below.
Click to Enlarge
Figure 1. Faraday Rotator's Effect on Linearly Polarized Light
Faraday Rotation
β = V x B x d
V: the Verdet Constant, a property of the optical material, in radians/T • m.
B: the magnetic flux density in teslas.
d: the path length through the optical material in meters.
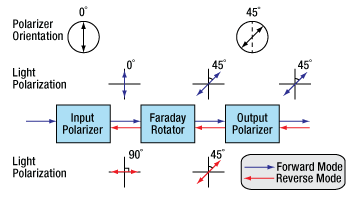
An optical isolator consists of an input polarizer, a Faraday rotator with magnet, and an output polarizer. The input polarizer works as a filter to allow only linearly polarized light into the Faraday rotator. The Faraday element rotates the input light's polarization by 45°, after which it exits through another linear polarizer. The output light is now rotated by 45° with respect to the input signal. In the reverse direction, the Faraday rotator continues to rotate the light's polarization in the same direction that it did in the forward direction so that the polarization of the light is now rotated 90° with respect to the input signal. This light's polarization is now perpendicular to the transmission axis of the input polarizer, and as a result, the energy is either reflected or absorbed depending on the type of polarizer.
Click to Enlarge
Figure 2. A single-stage, polarization-dependent isolator. Light propagating in the reverse direction is rejected by the input polarizer.
Polarization-Dependent Isolators
The Forward Mode
In this example, we will assume that the input polarizer's axis is vertical (0° in Figure 2). Laser light, either polarized or unpolarized, enters the input polarizer and becomes vertically polarized. The Faraday rotator will rotate the plane of polarization (POP) by 45° in the positive direction. Finally, the light exits through the output polarizer which has its axis at 45°. Therefore, the light leaves the isolator with a POP of 45°.
In a dual-stage isolator, the light exiting the output polarizer is sent through a second Faraday rotator followed by an additional polarizer in order to achieve greater isolation than a single-stage isolator.
The Reverse Mode
Light traveling backwards through the isolator will first enter the output polarizer, which polarizes the light at 45° with respect to the input polarizer. It then passes through the Faraday rotator rod, and the POP is rotated another 45° in the positive direction. This results in a net rotation of 90° with respect to the input polarizer, and thus, the POP is now perpendicular to the transmission axis of the input polarizer. Hence, the light will either be reflected or absorbed.
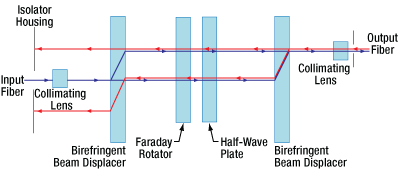 Click for Details
Click for DetailsFigure 3. A single-stage, polarization-independent isolator. Light is deflected away from the input path and stopped by the housing.
Polarization-Independent Fiber Isolators
The Forward Mode
In a polarization independent fiber isolator, the incoming light is split into two branches by a birefringent crystal (see Figure 3). A Faraday rotator and a half-wave plate rotate the polarization of each branch before they encounter a second birefringent crystal aligned to recombine the two beams.
In a dual-stage isolator, the light then travels through an additional Faraday rotator, half-wave plate, and birefringent beam displacer before reaching the output collimating lens. This achieves greater isolation than the single-stage design.
The Reverse Mode
Back-reflected light will encounter the second birefringent crystal and be split into two beams with their polarizations aligned with the forward mode light. The faraday rotator is a non-reciprocal rotator, so it will cancel out the rotation introduced by the half wave plate for the reverse mode light. When the light encounters the input birefringent beam displacer, it will be deflected away from the collimating lens and into the walls of the isolator housing, preventing the reverse mode from entering the input fiber.
General Information
Damage Threshold
With 25 years of experience and 5 U.S. patents, our isolators typically have higher transmission and isolation than other isolators, and are smaller than other units of equivalent aperture. For visible to YAG laser Isolators, Thorlabs' Faraday Rotator crystal of choice is TGG (terbium-gallium-garnet), which is unsurpassed in terms of optical quality, Verdet constant, and resistance to high laser power. Thorlabs' TGG Isolator rods have been damage tested to 22.5 J/cm2 at 1064 nm in 15 ns pulses (1.5 GW/cm2), and to 20 kW/cm2 CW. However, Thorlabs does not bear responsibility for laser power damage that is attributed to hot spots in the beam.
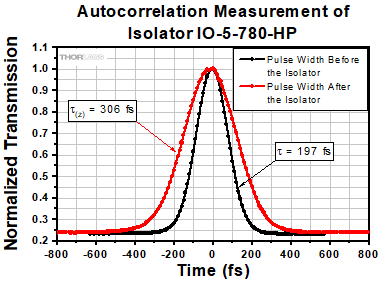
Click to Enlarge
Figure 4. Pulse Duration Measurements Before and After an IO-5-780-HP Isolator
Magnet
The magnet is a major factor in determining the size and performance of an isolator. The ultimate size of the magnet is not simply determined by magnetic field strength but is also influenced by the mechanical design. Many Thorlabs magnets are not simple one piece magnets but are complex assemblies. Thorlabs' modeling systems allow optimization of the many parameters that affect size, optical path length, total rotation, and field uniformity. Thorlabs' US Patent 4,856,878 describes one such design that is used in several of the larger aperture isolators for YAG lasers. Thorlabs emphasizes that a powerful magnetic field exists around these Isolators, and thus, steel or magnetic objects should not be brought closer than 5 cm.
Temperature
The magnets and the Faraday rotator materials both exhibit a temperature dependence. Both the magnetic field strength and the Verdet Constant decrease with increased temperature. For operation greater than ±10 °C beyond room temperature, please contact Technical Support.
Pulse Dispersion
Pulse broadening occurs anytime a pulse propagates through a material with an index of refraction greater than 1. This dispersion increases inversely with the pulse width and therefore can become significant in ultrafast lasers.
τ: Pulse Width Before Isolator
τ(z): Pulse Width After Isolator
Example:
τ = 197 fs results in τ(z) = 306 fs (pictured to the right)
τ = 120 fs results in τ(z) = 186 fs
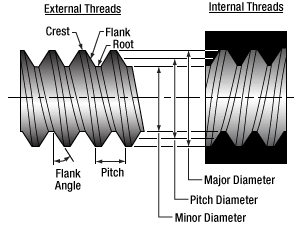
| SM05 Threading: Ø1/2" Lens Tubes, 16 mm Cage Systems | |||
|---|---|---|---|
| External Thread, 0.535"-40.0 UNS-2A | Internal Thread, 0.535"-40.0 UNS-2B | ||
| Max Major Diameter | 0.5340" | Min Major Diameter | 0.5350" |
| Min Major Diameter | 0.5289" | Min Pitch Diameter | 0.5188" |
| Max Pitch Diameter | 0.5178" | Max Pitch Diameter | 0.5230" |
| Min Pitch Diameter | 0.5146" | Min Minor Diameter (and 83.3% of Thread) | 0.508" |
| Max Minor Diameter | 0.5069" | Max Minor Diameter (and 64.9% of Thread) | 0.514" |
| RMS Threading: Objective, Scan, and Tube Lenses | |||
|---|---|---|---|
| External Thread, 0.800"-36.0 UNS-2A | Internal Thread, 0.800"-36.0 UNS-2B | ||
| Max Major Diameter | 0.7989" | Min Major Diameter | 0.8000" |
| Min Major Diameter | 0.7934" | Min Pitch Diameter | 0.7820" |
| Max Pitch Diameter | 0.7809" | Max Pitch Diameter | 0.7866" |
| Min Pitch Diameter | 0.7774" | Min Minor Diameter (and 83.3% of Thread) | 0.770" |
| Max Minor Diameter | 0.7688" | Max Minor Diameter (and 64.9% of Thread) | 0.777" |
| C-Mount Threading: Machine Vision Lenses, CCD/CMOS Cameras | |||
|---|---|---|---|
| External Thread, 1.000"-32.0 UN-2A | Internal Thread, 1.000"-32.0 UN-2B | ||
| Max Major Diameter | 0.9989" | Min Major Diameter | 1.0000" |
| Min Major Diameter | 0.9929" | Min Pitch Diameter | 0.9797" |
| Max Pitch Diameter | 0.9786" | Max Pitch Diameter | 0.9846" |
| Min Pitch Diameter | 0.9748" | Min Minor Diameter (and 83.3% of Thread) | 0.966" |
| Max Minor Diameter | 0.9651" | Max Minor Diameter (and 64.9% of Thread) | 0.974" |
| SM1 Threading: Ø1" Lens Tubes, 30 mm Cage Systems | |||
|---|---|---|---|
| External Thread, 1.035"-40.0 UNS-2A | Internal Thread, 1.035"-40.0 UNS-2B | ||
| Max Major Diameter | 1.0339" | Min Major Diameter | 1.0350" |
| Min Major Diameter | 1.0288" | Min Pitch Diameter | 1.0188" |
| Max Pitch Diameter | 1.0177" | Max Pitch Diameter | 1.0234" |
| Min Pitch Diameter | 1.0142" | Min Minor Diameter (and 83.3% of Thread) | 1.008" |
| Max Minor Diameter | 1.0068" | Max Minor Diameter (and 64.9% of Thread) | 1.014" |
| SM30 Threading: Ø30 mm Lens Tubes | |||
|---|---|---|---|
| External Thread, M30.5 x 0.5 – 6H/6g | Internal Thread, M30.5 x 0.5 – 6H/6g | ||
| Max Major Diameter | 30.480 mm | Min Major Diameter | 30.500 mm |
| Min Major Diameter | 30.371 mm | Min Pitch Diameter | 30.175 mm |
| Max Pitch Diameter | 30.155 mm | Max Pitch Diameter | 30.302 mm |
| Min Pitch Diameter | 30.059 mm | Min Minor Diameter (and 83.3% of Thread) | 29.959 mm |
| Max Minor Diameter | 29.938 mm | Max Minor Diameter (and 64.9% of Thread) | 30.094 mm |
| SM1.5 Threading: Ø1.5" Lens Tubes | |||
|---|---|---|---|
| External Thread, 1.535"-40 UNS-2A | Internal Thread, 1.535"-40 UNS-2B | ||
| Max Major Diameter | 1.5339" | Min Major Diameter | 1.535" |
| Min Major Diameter | 1.5288" | Min Pitch Diameter | 1.5188" |
| Max Pitch Diameter | 1.5177" | Max Pitch Diameter | 1.5236" |
| Min Pitch Diameter | 1.5140" | Min Minor Diameter (and 83.3% of Thread) | 1.508" |
| Max Minor Diameter | 1.5068" | Max Minor Diameter (and 64.9% of Thread) | 1.514" |
| SM2 Threading: Ø2" Lens Tubes, 60 mm Cage Systems | |||
|---|---|---|---|
| External Thread, 2.035"-40.0 UNS-2A | Internal Thread, 2.035"-40.0 UNS-2B | ||
| Max Major Diameter | 2.0338" | Min Major Diameter | 2.0350" |
| Min Major Diameter | 2.0287" | Min Pitch Diameter | 2.0188" |
| Max Pitch Diameter | 2.0176" | Max Pitch Diameter | 2.0239" |
| Min Pitch Diameter | 2.0137" | Min Minor Diameter (and 83.3% of Thread) | 2.008" |
| Max Minor Diameter | 2.0067" | Max Minor Diameter (and 64.9% of Thread) | 2.014" |
| SM3 Threading: Ø3" Lens Tubes | |||
|---|---|---|---|
| External Thread, 3.035"-40.0 UNS-2A | Internal Thread, 3.035"-40.0 UNS-2B | ||
| Max Major Diameter | 3.0337" | Min Major Diameter | 3.0350" |
| Min Major Diameter | 3.0286" | Min Pitch Diameter | 3.0188" |
| Max Pitch Diameter | 3.0175" | Max Pitch Diameter | 3.0242" |
| Min Pitch Diameter | 3.0133" | Min Minor Diameter (and 83.3% of Thread) | 3.008" |
| Max Minor Diameter | 3.0066" | Max Minor Diameter (and 64.9% of Thread) | 3.014" |
| SM4 Threading: Ø4" Lens Tubes | |||
|---|---|---|---|
| External Thread, 4.035"-40 UNS-2A | Internal Thread, 4.035"-40.0 UNS-2B | ||
| Max Major Diameter | 4.0337" | Min Major Diameter | 4.0350" |
| Min Major Diameter | 4.0286" | Min Pitch Diameter | 4.0188" |
| Max Pitch Diameter | 4.0175" | Max Pitch Diameter | 4.0245" |
| Min Pitch Diameter | 4.0131" | Min Minor Diameter (and 83.3% of Thread) | 4.008" |
| Max Minor Diameter | 4.0066" | Max Minor Diameter (and 64.9% of Thread) | 4.014" |
| Item # | Damage Threshold | |
|---|---|---|
| I405R5 | CW | 62 W/cm at 405 nm |
| Pulsed | 75 MW/cm2 at 405 nm | |
| I488R3 | CW | 106 W/cm at 488 nm |
| Pulsed | 150 MW/cm2 at 488 nm | |
| I532R5 | CW | 185 W/cm at 532 nm |
| Pulsed | 150 MW/cm2 at 532 nm | |
| I633R5 | CW | 185 W/cm at 633 nm |
| Pulsed | 150 MW/cm2 at 633 nm | |
| I670R5 | CW | 185 W/cm at 670 nm |
| Pulsed | 150 MW/cm2 at 670 nm | |
| I780R5 | CW | 185 W/cm at 780 nm |
| Pulsed | 150 MW/cm2 at 780 nm | |
| I850R5 | CW | 185 W/cm at 850 nm |
| Pulsed | 150 MW/cm2 at 850 nm | |
| I980R5 | CW | 185 W/cm at 980 nm |
| Pulsed | 150 MW/cm2 at 980 nm | |
| I1030R3 | CW | 106 W/cm at 1030 nm |
| Pulsed | 150 MW/cm2 at 1030 nm | |
| I1064R3 | CW | 106 W/cm at 1064 nm |
| Pulsed | 150 MW/cm2 at 1064 nm | |
| I1170R5 | CW | 60 W/cm at 1170 nm |
| I1220R5 | CW | 60 W/cm at 1220 nm |
| I1310R5 | CW | 92.3 W/cm at 1310 nm |
| I1390R5 | CW | 92.3 W/cm at 1390 nm |
| I1480R5 | CW | 92.3 W/cm at 1480 nm |
| I1550R5 | CW | 92.3 W/cm at 1550 nm |
| I1650R5 | CW | 92.3 W/cm at 1650 nm |
| I1750R5 | CW | 92.3 W/cm at 1750 nm |
| I1850R5 | CW | 92.3 W/cm at 1850 nm |
| I1950R5 | CW | 92.3 W/cm at 1950 nm |
| I2050R5 | CW | 92.3 W/cm at 2050 nm |
Damage Threshold Data for Thorlabs' Faraday Rotators
The specifications to the right are measured data for Thorlabs' Faraday Rotators. The power density of your beam should be calculated in terms of W/cm. For an explanation of why the linear power density provides the best metric for long pulse and CW sources, please see below.
Laser Induced Damage Threshold Tutorial
The following is a general overview of how laser induced damage thresholds are measured and how the values may be utilized in determining the appropriateness of an optic for a given application. When choosing optics, it is important to understand the Laser Induced Damage Threshold (LIDT) of the optics being used. The LIDT for an optic greatly depends on the type of laser you are using. Continuous wave (CW) lasers typically cause damage from thermal effects (absorption either in the coating or in the substrate). Pulsed lasers, on the other hand, often strip electrons from the lattice structure of an optic before causing thermal damage. Note that the guideline presented here assumes room temperature operation and optics in new condition (i.e., within scratch-dig spec, surface free of contamination, etc.). Because dust or other particles on the surface of an optic can cause damage at lower thresholds, we recommend keeping surfaces clean and free of debris. For more information on cleaning optics, please see our Optics Cleaning tutorial.
Testing Method
Thorlabs' LIDT testing is done in compliance with ISO/DIS 11254 and ISO 21254 specifications.
First, a low-power/energy beam is directed to the optic under test. The optic is exposed in 10 locations to this laser beam for 30 seconds (CW) or for a number of pulses (pulse repetition frequency specified). After exposure, the optic is examined by a microscope (~100X magnification) for any visible damage. The number of locations that are damaged at a particular power/energy level is recorded. Next, the power/energy is either increased or decreased and the optic is exposed at 10 new locations. This process is repeated until damage is observed. The damage threshold is then assigned to be the highest power/energy that the optic can withstand without causing damage. A histogram such as that below represents the testing of one BB1-E02 mirror.

The photograph above is a protected aluminum-coated mirror after LIDT testing. In this particular test, it handled 0.43 J/cm2 (1064 nm, 10 ns pulse, 10 Hz, Ø1.000 mm) before damage.
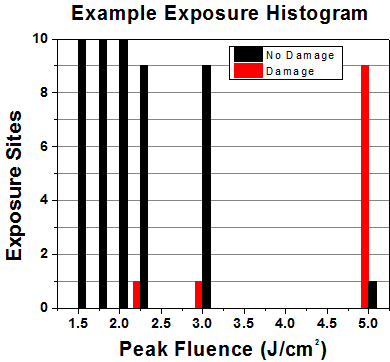
| Example Test Data | |||
|---|---|---|---|
| Fluence | # of Tested Locations | Locations with Damage | Locations Without Damage |
| 1.50 J/cm2 | 10 | 0 | 10 |
| 1.75 J/cm2 | 10 | 0 | 10 |
| 2.00 J/cm2 | 10 | 0 | 10 |
| 2.25 J/cm2 | 10 | 1 | 9 |
| 3.00 J/cm2 | 10 | 1 | 9 |
| 5.00 J/cm2 | 10 | 9 | 1 |
According to the test, the damage threshold of the mirror was 2.00 J/cm2 (532 nm, 10 ns pulse, 10 Hz, Ø0.803 mm). Please keep in mind that these tests are performed on clean optics, as dirt and contamination can significantly lower the damage threshold of a component. While the test results are only representative of one coating run, Thorlabs specifies damage threshold values that account for coating variances.
Continuous Wave and Long-Pulse Lasers
When an optic is damaged by a continuous wave (CW) laser, it is usually due to the melting of the surface as a result of absorbing the laser's energy or damage to the optical coating (antireflection) [1]. Pulsed lasers with pulse lengths longer than 1 µs can be treated as CW lasers for LIDT discussions.
When pulse lengths are between 1 ns and 1 µs, laser-induced damage can occur either because of absorption or a dielectric breakdown (therefore, a user must check both CW and pulsed LIDT). Absorption is either due to an intrinsic property of the optic or due to surface irregularities; thus LIDT values are only valid for optics meeting or exceeding the surface quality specifications given by a manufacturer. While many optics can handle high power CW lasers, cemented (e.g., achromatic doublets) or highly absorptive (e.g., ND filters) optics tend to have lower CW damage thresholds. These lower thresholds are due to absorption or scattering in the cement or metal coating.
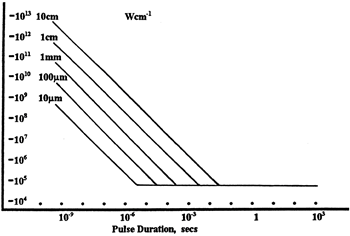
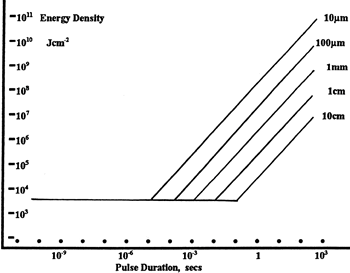
LIDT in linear power density vs. pulse length and spot size. For long pulses to CW, linear power density becomes a constant with spot size. This graph was obtained from [1].
Pulsed lasers with high pulse repetition frequencies (PRF) may behave similarly to CW beams. Unfortunately, this is highly dependent on factors such as absorption and thermal diffusivity, so there is no reliable method for determining when a high PRF laser will damage an optic due to thermal effects. For beams with a high PRF both the average and peak powers must be compared to the equivalent CW power. Additionally, for highly transparent materials, there is little to no drop in the LIDT with increasing PRF.
In order to use the specified CW damage threshold of an optic, it is necessary to know the following:
- Wavelength of your laser
- Beam diameter of your beam (1/e2)
- Approximate intensity profile of your beam (e.g., Gaussian)
- Linear power density of your beam (total power divided by 1/e2 beam diameter)
Thorlabs expresses LIDT for CW lasers as a linear power density measured in W/cm. In this regime, the LIDT given as a linear power density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size, as demonstrated by the graph to the right. Average linear power density can be calculated using the equation below.

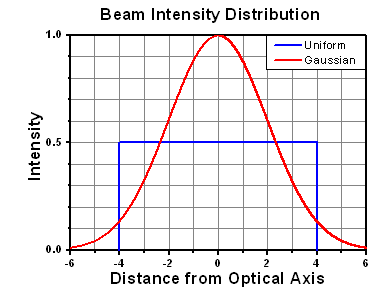
The calculation above assumes a uniform beam intensity profile. You must now consider hotspots in the beam or other non-uniform intensity profiles and roughly calculate a maximum power density. For reference, a Gaussian beam typically has a maximum power density that is twice that of the uniform beam (see lower right).
Now compare the maximum power density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately. A good rule of thumb is that the damage threshold has a linear relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 10 W/cm at 1310 nm scales to 5 W/cm at 655 nm):

While this rule of thumb provides a general trend, it is not a quantitative analysis of LIDT vs wavelength. In CW applications, for instance, damage scales more strongly with absorption in the coating and substrate, which does not necessarily scale well with wavelength. While the above procedure provides a good rule of thumb for LIDT values, please contact Tech Support if your wavelength is different from the specified LIDT wavelength. If your power density is less than the adjusted LIDT of the optic, then the optic should work for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. The damage analysis will be carried out on a similar optic (customer's optic will not be damaged). Testing may result in additional costs or lead times. Contact Tech Support for more information.
Pulsed Lasers
As previously stated, pulsed lasers typically induce a different type of damage to the optic than CW lasers. Pulsed lasers often do not heat the optic enough to damage it; instead, pulsed lasers produce strong electric fields capable of inducing dielectric breakdown in the material. Unfortunately, it can be very difficult to compare the LIDT specification of an optic to your laser. There are multiple regimes in which a pulsed laser can damage an optic and this is based on the laser's pulse length. The highlighted columns in the table below outline the relevant pulse lengths for our specified LIDT values.
Pulses shorter than 10-9 s cannot be compared to our specified LIDT values with much reliability. In this ultra-short-pulse regime various mechanics, such as multiphoton-avalanche ionization, take over as the predominate damage mechanism [2]. In contrast, pulses between 10-7 s and 10-4 s may cause damage to an optic either because of dielectric breakdown or thermal effects. This means that both CW and pulsed damage thresholds must be compared to the laser beam to determine whether the optic is suitable for your application.
| Pulse Duration | t < 10-9 s | 10-9 < t < 10-7 s | 10-7 < t < 10-4 s | t > 10-4 s |
|---|---|---|---|---|
| Damage Mechanism | Avalanche Ionization | Dielectric Breakdown | Dielectric Breakdown or Thermal | Thermal |
| Relevant Damage Specification | No Comparison (See Above) | Pulsed | Pulsed and CW | CW |
When comparing an LIDT specified for a pulsed laser to your laser, it is essential to know the following:
LIDT in energy density vs. pulse length and spot size. For short pulses, energy density becomes a constant with spot size. This graph was obtained from [1].
- Wavelength of your laser
- Energy density of your beam (total energy divided by 1/e2 area)
- Pulse length of your laser
- Pulse repetition frequency (prf) of your laser
- Beam diameter of your laser (1/e2 )
- Approximate intensity profile of your beam (e.g., Gaussian)
The energy density of your beam should be calculated in terms of J/cm2. The graph to the right shows why expressing the LIDT as an energy density provides the best metric for short pulse sources. In this regime, the LIDT given as an energy density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size. This calculation assumes a uniform beam intensity profile. You must now adjust this energy density to account for hotspots or other nonuniform intensity profiles and roughly calculate a maximum energy density. For reference a Gaussian beam typically has a maximum energy density that is twice that of the 1/e2 beam.
Now compare the maximum energy density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately [3]. A good rule of thumb is that the damage threshold has an inverse square root relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 1 J/cm2 at 1064 nm scales to 0.7 J/cm2 at 532 nm):
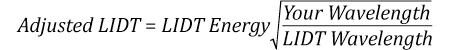
You now have a wavelength-adjusted energy density, which you will use in the following step.
Beam diameter is also important to know when comparing damage thresholds. While the LIDT, when expressed in units of J/cm², scales independently of spot size; large beam sizes are more likely to illuminate a larger number of defects which can lead to greater variances in the LIDT [4]. For data presented here, a <1 mm beam size was used to measure the LIDT. For beams sizes greater than 5 mm, the LIDT (J/cm2) will not scale independently of beam diameter due to the larger size beam exposing more defects.
The pulse length must now be compensated for. The longer the pulse duration, the more energy the optic can handle. For pulse widths between 1 - 100 ns, an approximation is as follows:
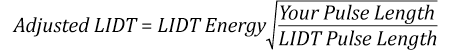
Use this formula to calculate the Adjusted LIDT for an optic based on your pulse length. If your maximum energy density is less than this adjusted LIDT maximum energy density, then the optic should be suitable for your application. Keep in mind that this calculation is only used for pulses between 10-9 s and 10-7 s. For pulses between 10-7 s and 10-4 s, the CW LIDT must also be checked before deeming the optic appropriate for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. Contact Tech Support for more information.
[1] R. M. Wood, Optics and Laser Tech. 29, 517 (1998).
[2] Roger M. Wood, Laser-Induced Damage of Optical Materials (Institute of Physics Publishing, Philadelphia, PA, 2003).
[3] C. W. Carr et al., Phys. Rev. Lett. 91, 127402 (2003).
[4] N. Bloembergen, Appl. Opt. 12, 661 (1973).
In order to illustrate the process of determining whether a given laser system will damage an optic, a number of example calculations of laser induced damage threshold are given below. For assistance with performing similar calculations, we provide a spreadsheet calculator that can be downloaded by clicking the button to the right. To use the calculator, enter the specified LIDT value of the optic under consideration and the relevant parameters of your laser system in the green boxes. The spreadsheet will then calculate a linear power density for CW and pulsed systems, as well as an energy density value for pulsed systems. These values are used to calculate adjusted, scaled LIDT values for the optics based on accepted scaling laws. This calculator assumes a Gaussian beam profile, so a correction factor must be introduced for other beam shapes (uniform, etc.). The LIDT scaling laws are determined from empirical relationships; their accuracy is not guaranteed. Remember that absorption by optics or coatings can significantly reduce LIDT in some spectral regions. These LIDT values are not valid for ultrashort pulses less than one nanosecond in duration.

A Gaussian beam profile has about twice the maximum intensity of a uniform beam profile.
CW Laser Example
Suppose that a CW laser system at 1319 nm produces a 0.5 W Gaussian beam that has a 1/e2 diameter of 10 mm. A naive calculation of the average linear power density of this beam would yield a value of 0.5 W/cm, given by the total power divided by the beam diameter:

However, the maximum power density of a Gaussian beam is about twice the maximum power density of a uniform beam, as shown in the graph to the right. Therefore, a more accurate determination of the maximum linear power density of the system is 1 W/cm.
An AC127-030-C achromatic doublet lens has a specified CW LIDT of 350 W/cm, as tested at 1550 nm. CW damage threshold values typically scale directly with the wavelength of the laser source, so this yields an adjusted LIDT value:

The adjusted LIDT value of 350 W/cm x (1319 nm / 1550 nm) = 298 W/cm is significantly higher than the calculated maximum linear power density of the laser system, so it would be safe to use this doublet lens for this application.
Pulsed Nanosecond Laser Example: Scaling for Different Pulse Durations
Suppose that a pulsed Nd:YAG laser system is frequency tripled to produce a 10 Hz output, consisting of 2 ns output pulses at 355 nm, each with 1 J of energy, in a Gaussian beam with a 1.9 cm beam diameter (1/e2). The average energy density of each pulse is found by dividing the pulse energy by the beam area:
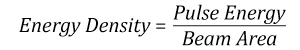
As described above, the maximum energy density of a Gaussian beam is about twice the average energy density. So, the maximum energy density of this beam is ~0.7 J/cm2.
The energy density of the beam can be compared to the LIDT values of 1 J/cm2 and 3.5 J/cm2 for a BB1-E01 broadband dielectric mirror and an NB1-K08 Nd:YAG laser line mirror, respectively. Both of these LIDT values, while measured at 355 nm, were determined with a 10 ns pulsed laser at 10 Hz. Therefore, an adjustment must be applied for the shorter pulse duration of the system under consideration. As described on the previous tab, LIDT values in the nanosecond pulse regime scale with the square root of the laser pulse duration:
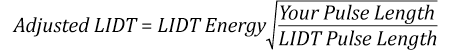
This adjustment factor results in LIDT values of 0.45 J/cm2 for the BB1-E01 broadband mirror and 1.6 J/cm2 for the Nd:YAG laser line mirror, which are to be compared with the 0.7 J/cm2 maximum energy density of the beam. While the broadband mirror would likely be damaged by the laser, the more specialized laser line mirror is appropriate for use with this system.
Pulsed Nanosecond Laser Example: Scaling for Different Wavelengths
Suppose that a pulsed laser system emits 10 ns pulses at 2.5 Hz, each with 100 mJ of energy at 1064 nm in a 16 mm diameter beam (1/e2) that must be attenuated with a neutral density filter. For a Gaussian output, these specifications result in a maximum energy density of 0.1 J/cm2. The damage threshold of an NDUV10A Ø25 mm, OD 1.0, reflective neutral density filter is 0.05 J/cm2 for 10 ns pulses at 355 nm, while the damage threshold of the similar NE10A absorptive filter is 10 J/cm2 for 10 ns pulses at 532 nm. As described on the previous tab, the LIDT value of an optic scales with the square root of the wavelength in the nanosecond pulse regime:
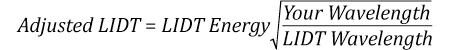
This scaling gives adjusted LIDT values of 0.08 J/cm2 for the reflective filter and 14 J/cm2 for the absorptive filter. In this case, the absorptive filter is the best choice in order to avoid optical damage.
Pulsed Microsecond Laser Example
Consider a laser system that produces 1 µs pulses, each containing 150 µJ of energy at a repetition rate of 50 kHz, resulting in a relatively high duty cycle of 5%. This system falls somewhere between the regimes of CW and pulsed laser induced damage, and could potentially damage an optic by mechanisms associated with either regime. As a result, both CW and pulsed LIDT values must be compared to the properties of the laser system to ensure safe operation.
If this relatively long-pulse laser emits a Gaussian 12.7 mm diameter beam (1/e2) at 980 nm, then the resulting output has a linear power density of 5.9 W/cm and an energy density of 1.2 x 10-4 J/cm2 per pulse. This can be compared to the LIDT values for a WPQ10E-980 polymer zero-order quarter-wave plate, which are 5 W/cm for CW radiation at 810 nm and 5 J/cm2 for a 10 ns pulse at 810 nm. As before, the CW LIDT of the optic scales linearly with the laser wavelength, resulting in an adjusted CW value of 6 W/cm at 980 nm. On the other hand, the pulsed LIDT scales with the square root of the laser wavelength and the square root of the pulse duration, resulting in an adjusted value of 55 J/cm2 for a 1 µs pulse at 980 nm. The pulsed LIDT of the optic is significantly greater than the energy density of the laser pulse, so individual pulses will not damage the wave plate. However, the large average linear power density of the laser system may cause thermal damage to the optic, much like a high-power CW beam.
| Posted Comments: | |
sandy champ
(posted 2022-02-21 16:20:13.207) HI,
What is the thickness or length of isolator? i mean the path length of optical material in meters?
Thickness in the following formula.
faraday rotation= verdet cont*B*thickness jdelia
(posted 2022-02-24 04:36:34.0) Thank you for contacting Thorlabs. These dimensions would depend on which specific Faraday Rotator have in mind. I have reached out to you directly to discuss this further. Dong IL Lee
(posted 2022-02-03 20:09:39.98) Dear Thorlabs company,
Is it possible to request a customized product that rotates the polarization of 22.5° or another degree?
Thanks,
Dong IL Lee cdolbashian
(posted 2022-02-10 12:02:14.0) Thank you for reaching out to us Dong! It is certainly possible to do this. I have contacted you directly to discuss the specifics of your custom rotator. In the future, if you have a custom request, feel free to contact our Solutions Team directly via TechSales@thorlabs.com. Al Scott
(posted 2022-02-01 09:44:44.57) What is the magnetic dipole moment of the Faraday rotators and can stray field be shielded for use of magnetic sensors nearby? cdolbashian
(posted 2022-02-24 04:06:01.0) Thank you for reaching out to us Al! Depending on the specific Faraday rotator selected, there will be a varying stray magnetic field generated from the pair of ring magnets used to magnetize the transparent rotation medium. Magnetic shielding is possible and I have contacted you directly to discuss your application and experimental geometry therein. Gemma Piquero
(posted 2021-11-26 05:15:04.93) Good morning!
Some time ago I bought a
I633R5 - 45 ° Faraday Rotator, CWL = 633 nm.
I am going to do an experiment with undergraduate students and I would like to know the constant Verdet of the material used.
Would you mind giving me more information about the material, the Verdet constant and its refractive indices?
Thank you in advance.
Sincerely,
Gemma YLohia
(posted 2021-12-07 11:25:37.0) Hello Gemma, thank you for contacting Thorlabs. The I633R5 contains TGG (Terbium Gallium Garnet), which has a Verdet constant of -134 Rad T^-1 m^-1 @ 632 nm (typically). Junghyun Park
(posted 2020-12-28 06:02:58.897) I have a question on the Faraday rotators (I524R5, I633R5, I780R5, I1064R5, I1550R5). I think there needs to be layers that induce the magnetic field through the Faraday rotators. However, I don't see any external active source (applied bias or permanent magnet) in the figure ("Application Idea"). Could you let me know where the external active power can be applied? YLohia
(posted 2020-12-29 03:50:26.0) Thank you for contacting Thorlabs. These Faraday Rotators do not contain active magnets. They do, however, contain strong permanent magnets that do not require external power. |

| Item # | Center Wavelength |
Operating Range |
Aperture | Faraday Rotationa |
Minimum Transmissiona |
Max Beam Diameter |
Max Power |
Damage Threshold | Dimensions (D x L) |
|---|---|---|---|---|---|---|---|---|---|
| I405R5 | 405 nm | 395 - 415 nm | 5.0 mm | 45° ± 3° | 96% | 4.7 mm | 20 W | 62 W/cm (CW) 75 MW/cm2 (Pulsed) |
Ø1.20" x 1.15" (Ø30.5 mm x 29.2 mm) |
| I488R3 | 488 nm | 468 - 508 nm | 3.0 mm | 45° ± 3° | 96% | 2.7 mm | 30 W | 106 W/cm (CW) 150 MW/cm2 (Pulsed) |
Ø1.20" x 2.65" (Ø30.5 mm x 67.2 mm) |
| I532R5 | 532 nm | 510 - 550 nm | 5.0 mm | 45° ± 3° | 95.5% | 4.7 mm | 40 W | 185 W/cm (CW) 150 MW/cm2 (Pulsed) |
Ø1.20" x 1.15" (Ø30.5 mm x 29.2 mm) |
| I633R5 | 633 nm | 603 - 663 nm | 5.0 mm | 45° ± 3° | 98% | 4.7 mm | 40 W | 185 W/cm (CW) 150 MW/cm2 (Pulsed) |
|
| I670R5 | 670 nm | 640 - 700 nm | 5.0 mm | 45° ± 3° | 97% | 4.7 mm | 40 W | 185 W/cm (CW) 150 MW/cm2 (Pulsed) |

| Item # | Center Wavelength |
Operating Range |
Aperture | Faraday Rotationa |
Minimum Transmissiona |
Max Beam Diameter |
Max Power |
Damage Threshold | Dimensions (D x L) |
|---|---|---|---|---|---|---|---|---|---|
| I780R5 | 780 nm | 740 - 820 nm | 5.0 mm | 45° ± 3° | 97.5% | 4.7 mm | 40 W | 185 W/cm (CW) 150 MW/cm2 (Pulsed) |
Ø1.20" x 1.65" (Ø30.5 mm x 41.9 mm) |
| I850R5 | 850 nm | 810 - 890 nm | 5.0 mm | 45° ± 3° | 97% | 4.7 mm | 40 W | 185 W/cm (CW) 150 MW/cm2 (Pulsed) |
Ø1.20" x 1.65" (Ø30.5 mm x 41.9 mm) |
| I980R5 | 980 nm | 960 - 1000 nm | 5.0 mm | 45° ± 3° | 98% | 4.7 mm | 40 W | 185 W/cm (CW) 150 MW/cm2 (Pulsed) |
Ø1.20" x 2.15" (Ø30.5 mm x 54.6 mm) |
| I1030R3 | 1030 nm | 990 - 1070 nm | 3.0 mm | 45° ± 3° | 96% | 2.7 mm | 30 W | 106 W/cm (CW) 150 MW/cm2 (Pulsed) |
Ø1.20" x 2.65" (Ø30.5 mm x 67.2 mm) |
| I1064R3 | 1064 nm | 1020 - 1100 nm | 3.0 mm | 45° ± 3° | 97.5% | 2.7 mm | 30 W | 106 W/cm (CW) 150 MW/cm2 (Pulsed) |
Ø1.20" x 2.65" (Ø30.5 mm x 67.2 mm) |

| Item # | Center Wavelength |
Operating Range |
Aperture | Faraday Rotationa |
Minimum Transmissiona |
Max Beam Diameter |
Max Power |
Damage Threshold | Dimensions (D x L) |
|---|---|---|---|---|---|---|---|---|---|
| I1170R5 | 1170 nm | 1120 - 1220 nm | 5.0 mm | 45° ± 2° | 98% | 4.7 mm | 10 W | 60 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
| I1220R5 | 1220 nm | 1170 - 1270 nm | 5.0 mm | 45° ± 2° | 98% | 4.7 mm | 10 W | 60 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
| I1310R5 | 1310 nm | 1260 - 1360 nm | 5.0 mm | 45° ± 1° | 98% | 4.7 mm | 15 W | 92.3 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
| I1390R5 | 1390 nm | 1340 - 1440 nm | 5.0 mm | 45° ± 1° | 98% | 4.7 mm | 15 W | 92.3 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
| I1480R5 | 1480 nm | 1430 - 1530 nm | 5.0 mm | 45° ± 1° | 98% | 4.7 mm | 15 W | 92.3 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
| I1550R5 | 1550 nm | 1500 - 1600 nm | 5.0 mm | 45° ± 1° | 98% | 4.7 mm | 15 W | 92.3 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
| I1650R5 | 1650 nm | 1600 - 1700 nm | 5.0 mm | 45° ± 2° | 98% | 4.7 mm | 15 W | 92.3 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
| I1750R5 | 1750 nm | 1700 - 1800 nm | 5.0 mm | 45° ± 3° | 97% | 4.7 mm | 15 W | 92.3 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
| I1850R5 | 1850 nm | 1800 - 1900 nm | 5.0 mm | 45° ± 3° | 96% | 4.7 mm | 15 W | 92.3 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
| I1950R5 | 1950 nm | 1900 - 2000 nm | 5.0 mm | 45° ± 3° | 97% | 4.7 mm | 15 W | 92.3 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
| I2050R5 | 2050 nm | 2000 - 2100 nm | 5.0 mm | 45° ± 3° | 97% | 4.7 mm | 15 W | 92.3 W/cm (CW) | Ø1.20" x 0.65" (Ø30.5 mm x 16.5 mm) |
 Products Home
Products Home










 Faraday Rotators
Faraday Rotators